贝叶斯公式：从条件概率到贝叶斯推断

一、什么是条件概率

在概率论中，我们经常要计算一个事件在另一个事件已经发生的条件下的概率，这就是条件概率。记做 P(A|B)，读作“在 B 发生的条件下 A 发生的概率”，其中 A 和 B 都是事件。条件概率的计算公式如下：

P(A|B) = P(A∩B) / P(B)

其中，P(A∩B) 表示 A 和 B 同时发生的概率，P(B) 表示 B 发生的概率。

二、什么是贝叶斯公式

贝叶斯公式是一种常用的条件概率公式，它是由英国数学家托马斯·贝叶斯（Thomas Bayes）提出的。贝叶斯公式用于计算事件 A 在给定事件 B 的条件下发生的概率。具体地说，贝叶斯公式的表达式如下：

P(A|B) = P(B|A) * P(A) / P(B)

其中，P(A|B) 表示事件 B 发生的条件下事件 A 发生的概率，P(B|A) 表示事件 A 发生的条件下事件 B 发生的概率，P(A) 表示事件 A 发生的概率，P(B) 表示事件 B 发生的概率。

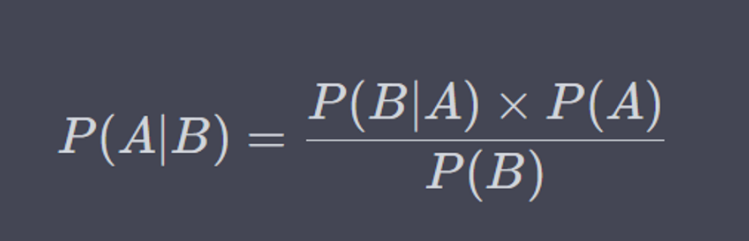
三、贝叶斯公式的应用

1、机器学习

在机器学习中，贝叶斯公式被广泛应用于朴素贝叶斯算法中。朴素贝叶斯算法是一种基于贝叶斯公式和假设特征之间相互独立的朴素性假设的分类算法。该算法通过计算在给定类别的条件下每个特征的概率，来预测一个未知样本属于哪个类别。

2、自然语言处理

在自然语言处理中，贝叶斯公式被应用于语言模型的构建中。语言模型是用于计算一个句子或文本的概率的模型。通过贝叶斯公式，可以计算一个句子或文本在给定上下文条件下的概率，从而判断它是否合理。

3、信号处理

在信号处理中，贝叶斯公式被应用于估计未知参数的概率分布。通过贝叶斯公式，可以将已知数据和先验信息结合起来，得到未知参数的后验概率分布，从而对未知参数进行估计。

四、总结

贝叶斯公式是一种重要的条件概率公式，它

可以用于各种领域的问题求解。在机器学习、自然语言处理和信号处理等领域，贝叶斯公式是一种重要的工具和方法。通过对贝叶斯公式的理解和应用，可以更好地解决实际问题。

需要注意的是，贝叶斯公式需要有先验概率的输入，也就是对于事件 A 的概率已经有一定的先验知识。在实际应用中，这些先验知识可以来自于历史数据、专家经验或其他领域知识。因此，选择合适的先验概率对于正确求解问题非常重要。

此外，贝叶斯公式也有其局限性。一般情况下，它只适用于处理简单的模型和问题，而对于复杂的模型和问题，可能需要更加高级的概率模型和算法。此外，在应用贝叶斯公式时，还需要注意数据量的大小、特征的选择等因素，以避免过拟合和欠拟合等问题。

综上所述，贝叶斯公式是一种非常有用的工具，它可以帮助我们更好地解决各种实际问题。同时，我们需要充分理解其概念和应用，并根据具体问题选择合适的先验知识和模型，以获得更加准确的结果。